
Calculate beam load and supporting forces
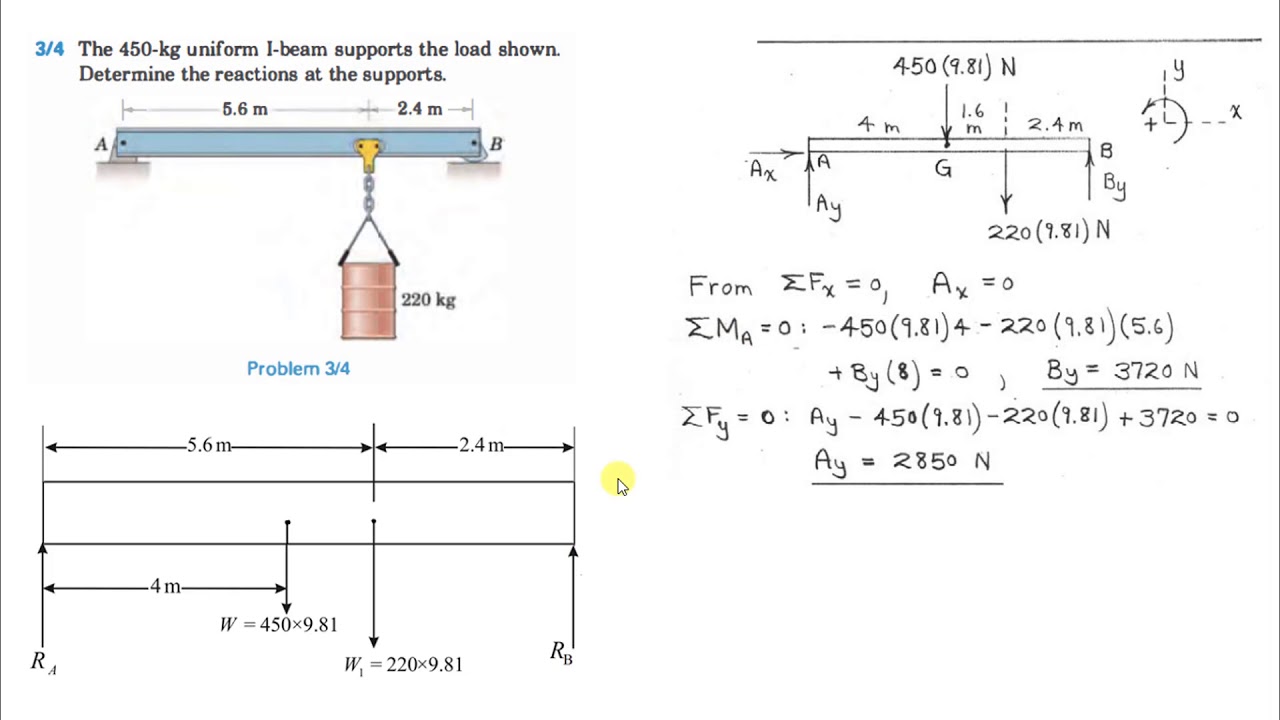
Similar calculations as above. I assume each meter of the beam has dimensions of 230 mm x 450 mm excluding slab thickness. So, self-weight can be around 2.5 kN per running meter. The density of bricks varies between 1500 to 2000 kg per cubic meter. The 450-kg uniform I-beam supports the load as shown in the attached diagram. How many reactions are in supports A and B respectively?-axis is to the right and the positive -axis is upward. One vertical and one horizontal forces in A and one vertical force and one moment in B; B.
Online Beam Support Force Calculator
The calculator below can be used to calculate the support forces - R1 and R2 - for beams with up to 6 asymmetrically loads.
For a beam in balance loaded with weights (or other load forces) the reactions forces - R - at the supports equals the load forces -F. The force balance can be expressed as
F1 + F2 + .... + Fn = R1 + R2 (1)
where
F = force from load (N, lbf)
R = force from support (N, lbf)
In addition for a beam in balance the algebraic sum of moments equals zero. The moment balance can be expressed as
F1 af1 + F2 af2 + .... + Fn afn = R ar1 + R ar2 (2)
where
a = the distance from the force to a common reference - usually the distance to one of the supports (m, ft)
Example - A beam with two symmetrical loads
A 10 m long beam with two supports is loaded with two equal and symmetrical loads F1 and F2 , each 500 kg. The support forces F3 and F4 can be calculated
(500 kg) (9.81 m/s2) + (500 kg) (9.81 m/s2) = R1 + R2
=>
R1 + R2 = 9810 N
= 9.8 kN
Note! Load due to the weight of a mass - m - is mg Newton's - where g = 9.81 m/s2.
With symmetrical and equal loads the support forces also will be symmetrical and equal. Using
R1 = R2
the equation above can be simplified to
R1 = R2 = (9810 N) / 2
= 4905 N
= 4.9 kN
Related Mobile Apps from The Engineering ToolBox
- free apps for offline use on mobile devices.
Example - A beam with two not symmetrical loads
A 10 m long beam with two supports is loaded with two loads, 500 kg is located 1 m from the end (R1), and the other load of 1000 kg is located 6 m from the same end. The balance of forces can be expressed as
(500 kg) (9.81 m/s2) + (1000 kg) (9.81 m/s2) = R1 + R2
=>
R1 + R2 = 14715 N
= 14.7 kN
The algebraic sum of moments (2) can be expressed as
(500 kg) (9.81 m/s2) (1 m) + (1000 kg) (9.81 m/s2) (6 m) =?R1 (0 m) + R2 (10 m)
=>
R2 = 6377 (N)
= 6.4 kN
F3can be calculated as:
R1= (14715 N) - (6377 N)
= 8338 N
= 8.3 kN
Insert beams to your Sketchup model with the Engineering ToolBox Sketchup Extension
Related Topics

- Mechanics - Forces, acceleration, displacement, vectors, motion, momentum, energy of objects and more
- Beams and Columns - Deflection and stress, moment of inertia, section modulus and technical information of beams and columns
- Statics - Loads - force and torque, beams and columns
Related Documents
- Aluminum I-Beams - Dimensions and static properties of aluminum I-beams - Imperial units
- American Standard Beams - S Beam - American Standard Beams ASTM A6 - Imperial units
- American Standard Steel C Channels - Dimensions and static parameters of American Standard Steel C Channels
- American Wide Flange Beams - American Wide Flange Beams ASTM A6 in metric units
- American Wide Flange Beams - W Beam - Dimensions of American Wide Flange Beams ASTM A6 - Imperial units
- Beams - Fixed at Both Ends - Continuous and Point Loads - Support loads, stress and deflections
- Beams - Fixed at One End and Supported at the Other - Continuous and Point Loads - Support loads, moments and deflections
- Beams - Supported at Both Ends - Continuous and Point Loads - Support loads, stress and deflections
- British Universal Columns and Beams - Properties of British Universal Steel Columns and Beams
- Cantilever Beams - Moments and Deflections - Maximum reaction force, deflection and moment - single and uniform loads
- Continuous Beam - Moment and Reaction Support Forces - Moment and reaction support forces with distributed or point loads
- Drawbridge Elevation - Forces and Moments - Calculate elevation moment for a drawbridge or a beam
- Equilibrant - The force required to keep a system of forces in equilibrium
- HE-A Steel Beams - Properties of HE-A profiled steel beams
- HE-B Steel Beams - Properties of HE-B profiled steel beams
- HE-M Steel Beams - Properties of HE-M profile steel beams
- Normal Flange I Beams - Properties of normal flange I profile steel beams
- Square Hollow Structural Sections - HSS - Weight, cross sectional area, moments of inertia - Imperial units
- Steel Angles - Equal Legs - Dimensions and static parameters of steel angles with equal legs - imperial units
- Steel Angles - Equal Legs - Dimensions and static parameters of steel angles with equal legs - metric units
- Steel Angles with Unequal Legs - Dimensions and static parameters of steel angles with unequal legs - imperial units
- Steel Angles with Unequal Legs - Dimensions and static parameters of steel angles with unequal legs - metric units
- Steel Pipe Columns - Allowable Loads - Allowable concentric loads for steel pipe columns
- Triangle - Triangle analytical geometry
- Trusses - Common types of trusses
- Weight of Beam - Stress and Strain - Stress and deformation of a vertical beam due to it's own weight
Tag Search
- en: beams calculation load weight forces supports
- es: vigas fuerzas cálculo de peso de carga soportes
- de: Balken Rechenlast Gewichtskräfte Stützen
The 450 Kg Uniform I Beams
Properties of HE-B profiled steel beams
Properties of HE-B steel beams according DIN 1025 and Euronorm 53-62
For full table with Static Parameters - Moment of Inertia and Elastic Section Modulus - rotate the screen!
| HEB | Dimensions | Static Parameters | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Moment of Inertia | Elastic Section Modulus | ||||||||
| Depth - h - (mm) | Width - w - (mm) | Web Thickness - s - (mm) | Sectional Area (cm2) | Mass (kg/m) | - Ix - (cm4) | - Iy - (cm4) | - Sx - (cm3) | - Sy - (cm3) | |
| 100B | 100 | 100 | 6 | 26 | 20.4 | 450 | 167 | 89.9 | 33.5 |
| 120B | 120 | 120 | 6.5 | 34 | 26.7 | 864 | 318 | 144 | 52.9 |
| 140B | 140 | 140 | 7 | 43 | 33.7 | 1510 | 550 | 216 | 78.5 |
| 160B | 160 | 160 | 8 | 54.3 | 42.6 | 2490 | 889 | 311 | 111 |
| 180B | 180 | 180 | 8.5 | 65.3 | 51.2 | 3830 | 1360 | 426 | 151 |
| 200B | 200 | 200 | 9 | 78.1 | 61.3 | 5700 | 2000 | 570 | 200 |
| 220B | 220 | 220 | 9.5 | 91 | 71.5 | 8090 | 2840 | 736 | 258 |
| 240B | 240 | 240 | 10 | 106 | 83.2 | 11260 | 3920 | 938 | 327 |
| 260B | 260 | 260 | 10 | 118 | 93 | 14920 | 5130 | 1150 | 395 |
| 280B | 280 | 280 | 10.5 | 131 | 103 | 19270 | 6590 | 1380 | 471 |
| 300B | 300 | 300 | 11 | 149 | 117 | 25170 | 8560 | 1680 | 571 |
| 320B | 320 | 300 | 11.5 | 161 | 127 | 30820 | 9240 | 1930 | 616 |
| 340B | 340 | 300 | 12 | 171 | 134 | 36660 | 9690 | 2160 | 646 |
- 1 cm4 = 104 mm4 = 10-8 m4 = 0.024 in4
- 1 cm3 = 103 mm3 = 10-6 m3 = 0.061 in3
- 1 cm2 = 102 mm2 = 10-4 m2 = 0.16 in2
- 1 kg/m = 0.67 lb/ft
The 450 Kg Uniform I Beam Dimensions
I-shaped cross-section beams:
- Britain : Universal Beams (UB) and Universal Columns (UC)
- Europe : IPE. HE. HL. HD and other sections
- US : Wide Flange (WF) and H sections
Related Topics
- Mechanics - Forces, acceleration, displacement, vectors, motion, momentum, energy of objects and more
- Beams and Columns - Deflection and stress, moment of inertia, section modulus and technical information of beams and columns
Related Documents
- Aluminum I-Beams - Dimensions and static properties of aluminum I-beams - Imperial units
- American Standard Beams - S Beam - American Standard Beams ASTM A6 - Imperial units
- American Wide Flange Beams - American Wide Flange Beams ASTM A6 in metric units
- American Wide Flange Beams - W Beam - Dimensions of American Wide Flange Beams ASTM A6 - Imperial units
- Area Moment of Inertia - Typical Cross Sections I - Area Moment of Inertia, Moment of Inertia for an Area or Second Moment of Area for typical cross section profiles
- Area Moment of Inertia - Typical Cross Sections II - Area Moment of Inertia, Moment of Inertia for an Area or Second Moment of Area for typical cross section profiles
- Beam Loads - Support Force Calculator - Calculate beam load and supporting forces
- Beams - Fixed at Both Ends - Continuous and Point Loads - Support loads, stress and deflections
- Beams - Fixed at One End and Supported at the Other - Continuous and Point Loads - Support loads, moments and deflections
- Beams - Supported at Both Ends - Continuous and Point Loads - Support loads, stress and deflections
- British Universal Columns and Beams - Properties of British Universal Steel Columns and Beams
- Cantilever Beams - Moments and Deflections - Maximum reaction force, deflection and moment - single and uniform loads
- Continuous Beam - Moment and Reaction Support Forces - Moment and reaction support forces with distributed or point loads
- HE-A Steel Beams - Properties of HE-A profiled steel beams
- HE-M Steel Beams - Properties of HE-M profile steel beams
- Normal Flange I Beams - Properties of normal flange I profile steel beams
- Steel Pipe Columns - Allowable Loads - Allowable concentric loads for steel pipe columns
Tag Search
The 450 Kg Uniform I Beam Conversion
- en: he-b steel beams din 1025 en 10034
- es: vigas de acero que-b din 1025 en 10.034
- de: er-b Stahlträger din 1025 en 10034
Comments are closed.